[수학 / Kotlin] BOJ 11050 ~ 11051 이항 계수 (1 ~ 2)

이항 계수 1

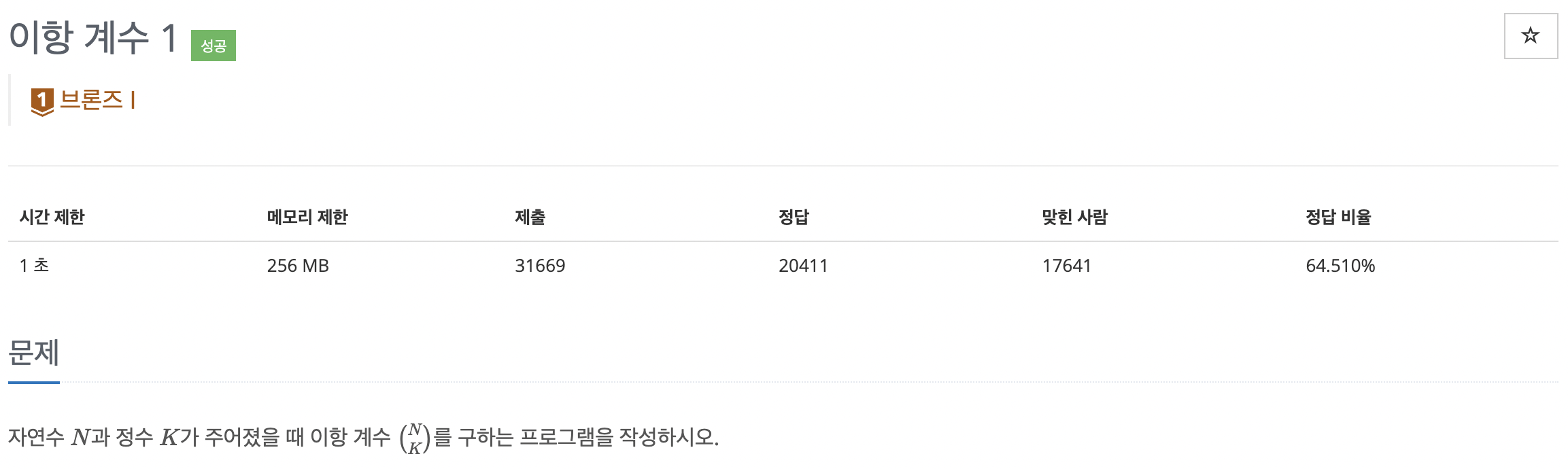
문제

풀이 언어

Kotiln

코드

import java.util.*

lateinit var array: Array<Int>
var n = 0
var k = 0

fun main() = with(Scanner(System.`in`)) {
    n = nextInt()
    k = nextInt()

    // 재귀 대신 DP로 팩토리얼 구현
    array = Array(n + 1) { 1 }

    // 팩토리얼 계산
    for (i in 2..n) {
        array[i] = array[i - 1] * i
    }

    // 조합 공식 적용
    // nCr = n! / (n-r)! * r!
    println(array[n] / (array[n - k] * array[k]))
}

풀이 방법

고등학교 때 배운 조합 공식 을 적용하면 어렵지 않게 해결할 수 있다.

결과

이항 계수 2

문제

코드

import java.util.*

lateinit var array: Array<Array<Int>>
var n = 0
var k = 0

fun main() = with(Scanner(System.`in`)) {
    n = nextInt()
    k = nextInt()

    // 파스칼의 삼각형을 사용하기 위한 배열 초기화
    array = Array(n + 1) { Array(n + 1) { 1 } }

    // nCr = n-1Ck-1 + n-1Ck
    for (i in 1..n) {
        for (j in 0..n) {
            if (i == j || j == 0) {
                array[i][j] = 1
            } else {
                array[i][j] = (array[i - 1][j - 1] + array[i - 1][j]) % 10007
            }
        }
    }

    println(array[n][k])
}

풀이 방법

이항 계수 1 보다 수가 커졌다. 단순히 DP 로 계산하면 Int 범위를 벗어나므로 터져버린다. Long 으로 계산해도 터져버린다. 문제에서 알려준 것처럼 모듈러 연산을 적용해야 한다. 처음에는 이전 문제에서 모듈러 나눗셈 을 적용하려 했는데 이 부분이 생각보다 까다로워서 일단 다른 방식으로 접근했다.

 

파스칼의 삼각형 을 적용했다.

나무위키 - 파스칼의 삼각형

결과

저작자표시비영리변경금지

'✍️ 코테 준비 > Math' 카테고리의 다른 글

[수학 / Kotlin] BOJ 11050 ~ 11051 이항 계수 (1 ~ 2)  (0)	2022.04.06