코드코도
[동적 계획법 1] [C++] 2579번. 계단 오르기 본문
2579번: 계단 오르기
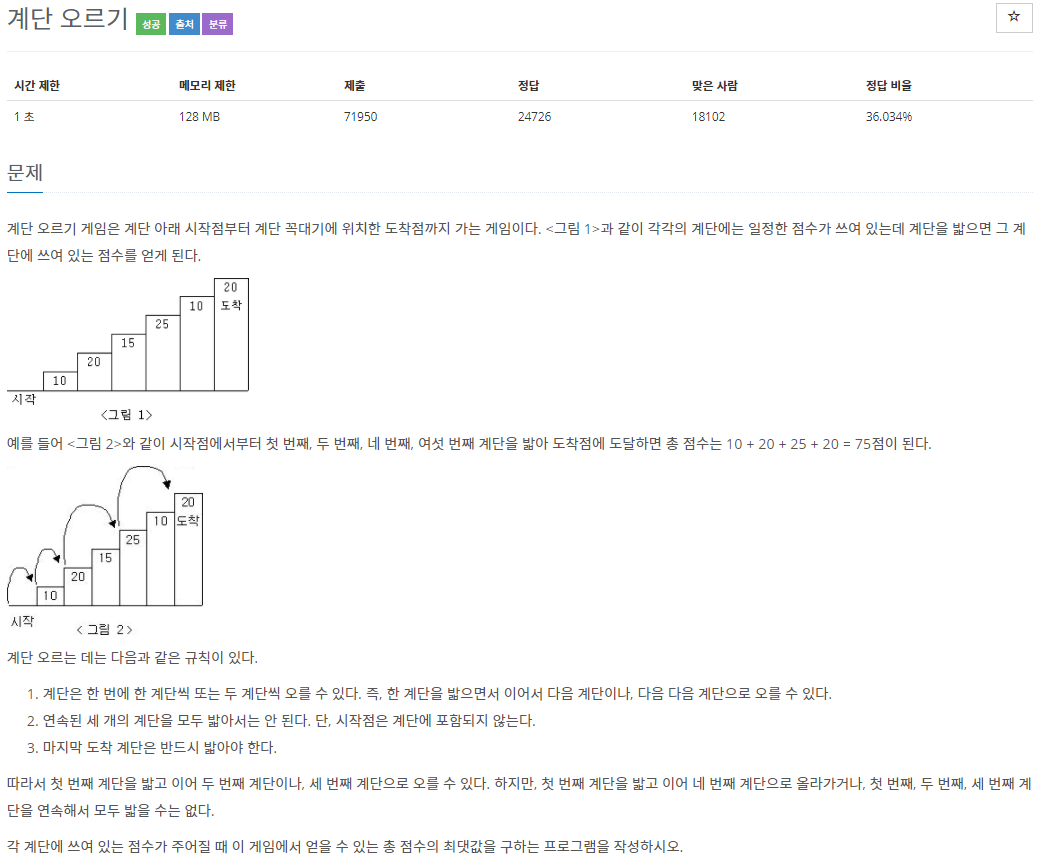
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
해결 방법
dp 문제이므로 점화식을 찾아야한다.
도착지점에 갈 수 있는 방법은 어떻게 될까? 두 가지로 나눌 수 있다.
i) 전 계단을 밟고 도착 지점을 밟는 경우
ii) 전전 계단을 밟고 도착 지점을 밟는 경우
이렇게 두 가지로 나눌 수 있는데 주의할 점은 연속된 3개의 계단은 밟을 수 없다는 것이다.
즉, i) 에서 전 계단을 밟기 이전에 전전 계단을 밟을 수 없고, 무조건 전전전 계단을 밟아야한다는 것이다.
따라서 이 조건을 점화식으로 나타내면
i) 전전전 계단의 최대값 + 전 계단 + 도착 계단 = dp[i-3] + stair[i-1] + stair[i]
ii) 전전 계단의 최대값 + 도착 계단 = dp[i-2] + stair[i]
위와 같이 나타낼 수 있다.
해결 과정
위의 점화식을 반복문을 통해 탐색하면 된다. 여기서 한 가지 더 주의할 점이 있다.
점화식을 살펴보면 dp[i-3], dp[i-2] 이므로 반복문의 시작 index 값을 i≥3 으로 잡아줘야 한다는 것이다.
따라서 dp[0], dp[1], dp[2]를 미리 선언해놓을 필요가 있다.
해당 계단까지의 최대 값을 저장해놓은 배열이 dp라고 할 때 아래와 같이 나타낼 수 있다.
dp[0] = stair[0]
dp[1] = max(stair[1], stair[0] + stair[1])
dp[2] = max(stair[0] + stair[1], stair[1] + stair[2])
여기서 max함수는 최대 값을 return하는 함수이다.
최종 코드는
#include <iostream>
using namespace std;
int max(int a, int b){
return a > b ? a : b;
}
int main(){
int n;
int stair[300], dp[300];
cin >> n;
for(int i = 0; i < n; i++){
cin >> stair[i];
}
dp[0] = stair[0];
dp[1] = max(stair[1], stair[0] + stair[1]);
dp[2] = max(stair[0] + stair[2], stair[1] + stair[2]);
for(int i = 3; i < n; i++){
dp[i] = max(dp[i-2] + stair[i], dp[i-3] + stair[i-1] + stair[i]);
}
cout << dp[n-1];
return 0;
}
'Boj > Dynamic Programming' 카테고리의 다른 글
| [동적 계획법 1] [C++] 10844번. 쉬운 계단 수 (0) | 2021.01.24 |
|---|---|
| [동적 계획법 1] [C++] 1463번. 1로 만들기 (0) | 2021.01.19 |
| [동적 계획법 1] [C++] 2579번. 계단 오르기 (0) | 2021.01.14 |
| [동적 계획법 1] [C++] 1932번. 정수 삼각형 (0) | 2021.01.13 |
| [동적 계획법 1] [C++] 1149번. RGB 거리 (0) | 2021.01.13 |
| [동적 계획법 1] [C++] 9461번. 파도반 수열 (0) | 2021.01.13 |
