Dijsktra (다익스트라)
최단 경로 탐색 - 1
정말 오랜만에 포스팅이다. 원래 목표대로 진행했으면 개강을 하기 전에 DP까지 포스팅을 했어야하는데 요새 조금 바빴다...(사실 의욕이 없던걸 수도...) 아무튼 이번 3-1 과목에 알고리즘 응용이라는 과목을 수강하는데 작년에는 딥러닝과 관련하여 수업했다고해서 신청했는데 이번에 교수님이 바뀌면서 정말 알고리즘에 대해 학습하는 수업이 되어버렸다. 살짝 아쉬웠지만 강의계획서를 보니 2-2 알고리즘 수업과 거의 비슷해서? 학기 초에 미리미리 정리해두려고 한다.
서론이 길었다.
다익스트라는 최단 경로를 탐색하는 알고리즘이다.
다음과 같은 그래프의 최단 경로를 탐색해보자.

graph 변수에 연결된 정점과 가중치가 저장되어 있다고 본다.
graph[1] = [2, 6], [3, 4], [4, 4]
graph[2] = [4, 5], [5, 7]
graph[3] = [6, 10]
graph[4] = []
graph[5] = [6, 2]
graph[6] = []
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Distance | 0 | INF | INF | INF | INF | INF |
| Visit | False | False | False | False | False | False |
우선 각 정점들간의 최단 거리를 저장할 변수가 필요하다.
이를 distance[1] ~ distance[6] 으로 나타내겠다.
추가로 distance 변수를 INF로 초기화를 해줘야한다.
아직 탐색하지 않았으므로 모든 정점들 간의 최단 거리가 INF라고 가정한다.
뿐만 아니라 방문한 정점임을 표시하기 위한 변수가 필요하다.
이를 visit[1] ~ visit[6] 으로 나타내겠다.
이 역시 아직 방문하지 않았으므로 False로 초기화를 해줘야한다.
| Queue | 1 |
Queue에는 시작 정점이 들어있고, distance[시작 정점] = 0으로 초기화 되어있다고 본다.
1. Queue에서 시작 정점을 제거하고 연결된 다른 정점들의 최단 거리를 갱신한다.
distance[2] = INF > distance[0] + 6 = 6 이므로 갱신이 가능하다.
따라서 distance[2] = 6 가 된다.
distance[3] = INF > distance[0] + 4 = 4 이므로 갱신이 가능하다.
따라서 distance[3] = 4 가 된다.
distance[4] = INF > distance[0] + 4 = 4 이므로 갱신이 가능하다.
따라서 distance[4] = 4 가 된다.
2. 갱신한 경우 해당 정점과 최단 거리를 Queue에 넣어준다.
우선순위큐를 사용하기 위해 파이썬의 heapq 라이브러리를 사용하였다. (최소힙)
| Queue | (6, 2) | (4, 3) | (4, 4) |
3. 해당 정점을 방문 처리 해준다.
과정이 종료되면 아래와 같이 변수 값이 변경된다.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Distance | 0 | 6 | 4 | 4 | INF | INF |
| Visit | True | False | False | False | False | False |
4. Queue에서 최단거리가 가장 짧은 정점을 제거하고 연결된 다른 정점들의 최단 거리를 갱신한다.
distance[6] = INF > distance[3] + 10 = 14 이므로 갱신이 가능하다.
따라서 distance[6] = 14 가 된다.
5. 갱신한 경우 해당 정점과 최단 거리를 Queue에 넣어준다.
| Queue | (6, 2) | (4, 4) | (14, 6) |
6. 해당 정점을 방문 처리 해준다.
과정이 종료되면 아래와 같이 변수 값이 변경된다.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Distance | 0 | 6 | 4 | 4 | INF | 14 |
| Visit | True | False | True | False | False | False |
7. 4 ~ 6 과정을 반복해준다.
8. 위 과정을 Queue에 원소가 없을 때까지 반복하며 과정이 종료되면 최종 형태는 아래와 같다.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Distance | 0 | 6 | 4 | 4 | 2 | 4 |
| Visit | True | True | True | True | True | True |
다익스트라 알고리즘에서 명심해야할 점은
1. 방문한 노드는 탐색하지 않는다.
2. 최단 거리가 짧은 정점부터 탐색해야한다.
3. 음의 사이클이 존재하는 경우 최단 거리 탐색이 정상적으로 진행되지 않는다.
이다.
위의 개념을 파이썬으로 구현해보았다. 주석과 함께 달아놓았으니 참고하길 바란다.
위에서 언급한 그래프로 입력 값을 주면 이론상으로 구한 답과 동일 한 것을 볼 수 있다.
[Input]
6 8 # 정점의 개수, 간선의 개수
1 2 3 4 5 6
1 2 6
1 3 4
1 4 4
1 5 2
2 4 5
2 5 7
3 6 10
5 6 2
1 # 시작 정점
[Output]
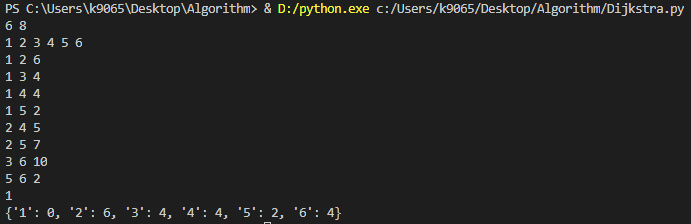
음의 사이클이 존재하는 경우는 다음 포스팅인 벨만포드 알고리즘을 통해 설명하도록 하겠다.
충남대학교 컴퓨터공학과 이영석 교수님의 알고리즘 수업과 동빈나의 유튜브 강좌(https://youtu.be/611B-9zk2o4)를 참고했습니다.
'✏️ 알고리즘 > Graph' 카테고리의 다른 글
| 6. Union Find(합집합 찾기) : MST - 1 (0) | 2021.05.30 |
|---|---|
| 5. Floyd Warshall(플루이드 와샬) : 최단 경로 탐색 - 3 (0) | 2021.03.31 |
| 4. Bellman-Ford(벨만 포드) : 최단 경로 탐색 - 2 (0) | 2021.03.07 |
| 2. DFS(Depth-Find-Search) : 깊이 우선 탐색 (0) | 2021.01.22 |
| 1. BFS(Breath-Find-Search) : 너비 우선 탐색 (0) | 2021.01.21 |