Union Find (합집합 찾기)
MST - 1
정말 오랜만에 포스팅이다.
MST 알고리즘 문제를 풀던 도중 생각나서 포스팅 하게 됐다.
매주 주말마다 알고리즘 개념 정리를 하려고 하는데 계속 실패하는 것 같다... ㅎㅎ;;
오늘 다뤄볼 주제는 MST, 최소 신장 트리 문제를 해결하기 위한 기본 베이스인 Union Find이다.
최소 신장 트리 문제를 해결하기 위한 방법에는 대표적으로 크루스칼(Kruskal)과 프림(Prim) 알고리즘이 존재한다.
Union FInd는 크루스칼 알고리즘의 핵심이라고 말할 수 있다.
그럼 Union Find가 무엇인지 알아보자.
Union Find는 말 그대로 Union, 집합을 찾는 알고리즘이다.
그래프 정보가 주어졌을 때 이들 간의 관계를 알아볼 수 있다.
바로 예시로 들어보자.

위와 같은 그래프 형태가 주어졌을 때 (1, 2, 3, 4)와 (5, 6)으로 분류할 수 있다.
이렇게 집합별로 분류할 수 있게 해주는 알고리즘이 Union Find이다.
Union Find를 진행하기 위해선 Union과 Find, 2개의 함수가 정의되어야 한다.
우선 Find를 먼저 알아보자.
Find는 부모 노드를 탐색하는 함수이다.
parents는 특정 노드의 부모 노드가 저장되어 있는 리스트이다.
재귀적으로 호출하면서 부모 노드 값을 리턴한다.
def find_parent(parents, x):
if parents[x] != x:
parents[x] = find_parent(parents, parents[x])
return parents[x]
Union은 두 개의 원소의 부모 노드를 비교하는 함수이다.
find를 이용해서 두 원소의 부모 노드를 찾아내고 이를 비교한다.
값이 같은 경우 사이클이 존재하는 경우이므로 1을 리턴하고 함수를 종료한다.
값이 다른 경우 더 작은 값을 부모 노드로 만들어준다. 이후 0을 리턴하고 함수를 종료한다.
def union_parent(parents, x, y):
x = find_parent(parents, x)
y = find_parent(parents, y)
if x == y: # 사이클이 발생한 경우
return 1
# 값이 작을수록 더 낮은 레벨의 노드
if x > y:
parents[x] = y # x의 부모 노드를 y로 바꿔준다.
else:
parents[y] = x # y의 부모 노드를 x로 바꿔준다.
return 0 # 정상적으로 합쳐진 경우값이 같은 경우 사이클이 존재한다고 판단하는 부분이 이해가 되지 않을수도 있다.
예를 들어 아래와 같이 입력 값이 주어진 경우
3 2 # 노드 개수, 간선 개수
1 2
1 3
2의 부모 노드도 1이고 3의 부모 노드도 1인데? 사이클로 결과가 출력되어야하는 것이 아닌가?
하지만 초기에 부모 노드가 담긴 리스트를 자기 자신으로 초기화 시켜주었기 때문에
처음 방문하는 노드인 경우 그 값이 자기 자신일 것이다. 따라서 if문 조건에 걸리지 않는다.
이게 끝이다. 모든 노드에 대해 Union과 Find를 해주면 된다.
위에서 말한 단계적으로 진행해보자.
1. 자기 자신을 부모 노드로 설정해준다.
| 현재 노드 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 노드 | 1 | 2 | 3 | 4 | 6 | 6 |
우선 특정 노드의 부모 노드를 자기 자신으로 설정해줄 필요가 있다. (초기화)
2. 노드를 탐색하면서 두 노드의 부모 노드를 비교한다. 더 작은 노드를 부모 노드로 정해준다.
3. 두 원소의 부모 노드가 같은 경우 이는 사이클이 존재하는 경우이므로 종료한다.
위의 개념을 파이썬으로 구현해보았다.
def find_parent(parents, x):
if parents[x] != x:
parents[x] = find_parent(parents, parents[x])
return parents[x]
def union_parent(parents, x, y):
x = find_parent(parents, x)
y = find_parent(parents, y)
if x == y: # 사이클이 발생한 경우
return 1
# 값이 작을수록 더 낮은 레벨의 노드
if x > y:
parents[x] = y # x의 부모 노드를 y로 바꿔준다.
else:
parents[y] = x # y의 부모 노드를 x로 바꿔준다.
return 0 # 정상적으로 합쳐진 경우
def main():
n, m = map(int, input().split())
nodes = [[] for _ in range(n+1)] # 1 ~ n까지의 노드 정보를 저장할 리스트
parents = [i for i in range(n+1)] # 부모노드를 저장할 리스트 -> 초기값은 자기 자신
for _ in range(m):
src, dst = map(int, input().split())
nodes[src].append(dst)
cycleCheck = False
for i in range(1, n+1):
for j in nodes[i]:
if union_parent(parents, i, j) == 1:
cycleCheck = True
break
if cycleCheck:
print("사이클이 발생했습니다!")
else:
print(parents[1:])
if __name__ == "__main__":
main()
실행 결과 부모 노드를 정확하게 탐색한 것을 확인할 수 있다.
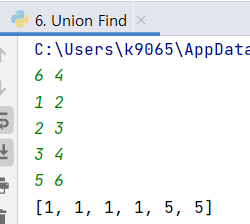
다음 시간엔 Union Find를 이용하여 MST를 계산하는 알고리즘인 Kruskal에 대해 포스팅을 해보겠다.
'✏️ 알고리즘 > Graph' 카테고리의 다른 글
| 5. Floyd Warshall(플루이드 와샬) : 최단 경로 탐색 - 3 (0) | 2021.03.31 |
|---|---|
| 4. Bellman-Ford(벨만 포드) : 최단 경로 탐색 - 2 (0) | 2021.03.07 |
| 3. Dijsktra(다익스트라) : 최단 경로 탐색 - 1 (0) | 2021.03.02 |
| 2. DFS(Depth-Find-Search) : 깊이 우선 탐색 (0) | 2021.01.22 |
| 1. BFS(Breath-Find-Search) : 너비 우선 탐색 (0) | 2021.01.21 |